Pearson Product-Moment Correlation
The Pearson product-moment correlation provides a measure of the degree of linear relationship between to variables that produce score data.
Listed below are data two variables (X and Y) for six people. We create two columns for the X and Y scores, two more columns for the squares of those scores, and a third column, which is called the cross-product. That column has the product of the X score times the Y score. We then compute the sums of all of those columns. Those values, together with the same size (N, which is equal to 5 in this case) is all that we need to compute the correlation.
| Person | X | Y | X2 | Y2 | XY |
| A | 4 | 6 | 16 | 36 | 24 |
| B | 2 | 3 | 4 | 9 | 6 |
| C | 3 | 6 | 9 | 36 | 18 |
| D | 5 | 7 | 25 | 49 | 35 |
| E | 5 | 8 | 25 | 64 | 40 |
| Sums | 19 | 30 | 79 | 194 | 123 |
To compute the correlation, we plug in the scores to the formula below, as shown. We use the notation rxy to indicate the correlation between the X and Y variables.
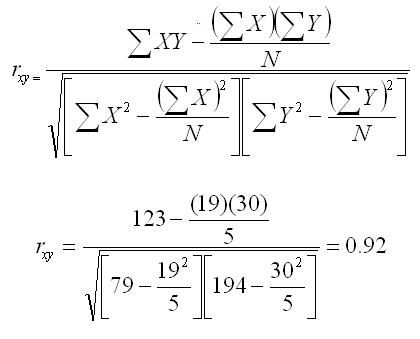
In order to evaluate this correlation, we must compare it to the critical value for the correlation. The critical value of r can be found in a table of critical values of the Pearson Product-Moment correlation. We have included a link to this table, but you can also find the table in most statistics textbooks.
The table presents the critical values by alpha level and degrees of freedom. The degrees of freedom for the Pearson product-moment correlation are equal to N - 2. If we assume an alpha of 0.05, the critical value of r is .8783. Because 0.92 exceeds the critical value of r, we conclude that there is a relationship between the two variables in the population from which the sample is drawn.
What we are doing by checking our computed correlation against the tabled critical value is testing to see whether the correlation is large enough that we would conclude that there is a relationship between these variables in the population from which the sample was drawn.