Comparing Two or More
Independent Samples
You have now learned procedures for comparing two groups using a t-test. The t-test that you use depends on whether the groups are correlated or independent. But when we have more than two groups in a study, we have to take a different approach to compare those groups.
The approach that we use was first developed by Sir Ronald Fisher (1935). It is called analysis of variance, which is often abbreviated as ANOVA. In this first section on ANOVA, we will look at comparing two or more independent groups, which are defined by their level of a single independent variable. The ANOVA that we use in such a situation is called a one-way ANOVA.
Logic of the ANOVA
ANOVAs are sometimes called F-tests, because they compute a test statistic called F. The test statistic is named after its creator, Sir Ronald Fisher. The F statistic is a ratio of variances. The numerator of the ratio is based on the variability of the means; the denominator of the ratio is based on the variability of scores within each group. We refer to these variances as the between-groups variability and the within-groups variability, respectively.
This approach may seem on the surface like it is completely different from the approach taken with the t-test, but it is actually based on identical logic. The denominator of the t-test is based on the variability within the groups, just as it is in the ANOVA. But what about the numerator in the t-test. Surely a mean difference has nothing to do with the variability of means.
If the null hypothesis is true, then the means were drawn from the same population with the same population mean. We know that, due to sampling error, the mean of each sample drawn will be close to the population mean, but is unlikely to be exactly equal to the population mean. In fact, we know that the if we sample repeatedly from a population, we will obtain a distribution of means, which we called the sampling distribution of means. The standard deviation of this distribution was our standard error, which was the numerator of the t-test.
If we draw two samples from the distribution of means, we know that they are not likely to be identical, even though under the null hypothesis that they were sampled from the same population. Therefore, the difference between these samples is unlikely to be zero. How big that difference would be by chance, if the null hypothesis is true, is predictable, because it is a function of how variable the sampling distribution of the means is. If this sample distribution is very narrow, the two means will always be close to one another, and so the mean difference necessarily must be small. But as the variability of the sampling distribution increases, the possibility of the means being different from one another increases.
The math is beyond the scope of this text, but there is a direct mathematical relationship between the variability of a sampling distribution of means and the average size of the difference between two means randomly drawn from that sampling distribution. In other words, the difference between the means (the numerator of the t-test) really is just a different way of measuring the variability among the two means.
So the t-test and the F-ratio of an ANOVA look like they are measuring very different things, but in fact, both are looking at the variability of means in the numerator and comparing it with a measure of the variability of scores within the groups in the denominator.
So if you have two groups in your study, you could conduct a t-test, but you could also conduct an ANOVA. Will these two tests lead you to the same conclusion? They will indeed. In fact, these two tests, which appear on the surface to be very different approaches, actually have a precise mathematical relationship with one another. If you take data from a study of two groups and compute both a t and an F-ratio, you will find the that the F is equal to t2. We will not show you the math that proves that F=t2, because it is well beyond the text, but you can try it for yourself with real data to see that it works.
In chapter 10, you were introduced to the concept of ANOVA from the standpoint of what variables contribute to the numerator and denominator of the F-ratio. The denominator of the F-ratio is a function of the nonsystematic within-groups variability, which is just another way of saying the population variance. When the null hypothesis is true, the numerator is also a function of this nonsystematic within-groups variability, because the variability of the means in the sampling distribution of the means is perfectly predictable if you know (1) the variability of the scores in the population and (2) the size of the sample. You learned that when we first introduced the concept of the sampling distribution of the mean.
The formulas for ANOVA convert the variability of the means (the numerator) onto the same scale as the variability of the scores within the groups (the denominator). Therefore, if the null hypothesis is true, both the numerator and the denominator of the F-ratio estimate the same quantity (the variance of scores in the population). Consequently, the F-ratio will be approximately equal to 1.00. Of course, sometimes it will be greater than 1.00 and sometimes it will be less than 1.00, so we need to know how much greater than 1.00 the F-ratio must be before we suspect that the null hypothesis is false. Just like with the t-test, there is a table of critical values of F that you can consult to answer this question. We will show you exactly how to do that shortly.
Chapter 10 also explained that any systematic differences between the groups in a study would increase the variability among the group means beyond what one would expect from sampling error alone, which would increase the size of the F-ratio. Chapter 10 made the distinction between experimental variance (due to the effects of the independent variable) and extraneous variance (due to the effects of confounding variables). This distinction is important in research design, because you cannot draw confident conclusions if you have not controlled potential confounding variables. However, from the standpoint of statistics, both are systematic effects and both will increase the numerator of the F-ratio beyond what you would get from sampling error alone. The statistics cannot separate these two effects, which is why you, as the researcher, must control confounding if you want to learn anything useful from your study.
Terminology
In an ANOVA, the variance estimates are called mean squares. So in a one-way ANOVA, in which we are testing for mean differences among groups defined by a single independent variable, we will have two mean squares: the mean square within groups (the denominator) and the mean square between groups (the numerator). Remember that the mean square within groups is a function of the nonsystematic within-groups variance and that the mean square between groups is a function of both the nonsystematic within-groups variance and any systematic effects due to the independent variable or uncontrolled confounding factors.
There are two different degrees of freedom (dfs) for a one-way ANOVA. One is associated with the numerator (called the between-groups df and written as dfb) and the other is associated with the denominator (called the within-groups df and written dfw).
Analysis of variance procedures were developed long before computers were available, and even calculators were uncommon when ANOVAs were first used. Therefore, some very systematic procedures were developed for organizing the calculations and providing internal checks of their accuracy.
This structure is still used, even though most ANOVAs are done by computer these days. The structure is called the ANOVA summary table, which lists the critical values that are computed for any given ANOVA. The format for this summary table for a one-way ANOVA is shown below.
ANOVA Summary Table for a One-Way ANOVA |
|||||
|
Source |
df | SS | MS | F | p |
| Between | dfb=k-1 | SSb | MSb=SSb/dfb |
F=MSb/MSw |
|
| Within | dfw=N-k | SSw | MSw=SSw/dfw | ||
| Total | dfT=N-1 | SST | |||
This table has several terms that will be new to you, so let's go through the table systematically and define everything.
The first column is the source of variation. In a simple one-way ANOVA, you have three sources of variation: between, within, and total. The between is based on the variability of the means, the within is based on the variability within the groups, and the total is based on the variability of all of the scores regardless of what group they came from. We do not use the total in the computation of the ANOVA except that it provides a check on the accuracy of computations, as you will see shortly.
The second column is the degrees of freedom. The between-groups degrees of freedom (dfb) is equal to the number of groups minus 1. Traditionally, the letter k is used to indicate the number of groups, so dfb = k-1. The dfw is equal to the total number of participants minus the number of groups (which is written as dfw = N-k). The dfT is equal to the total number of participants minus 1 (N - 1). A simple check on the accuracy of your computation of these degrees of freedom is that dfT should equal the sum of dfb and dfw.
The third column (labeled SS) lists the sums of squares. You were introduced to the sum of squares concept when you first learned about the variance. It is the numerator of the variance formula (short for sum of squared differences from the mean).
In ANOVAs, several sums of squares are computed, and again, they are the numerators for the variance estimates that we call mean squares. You will be introduced to the computational formulas for the sums of squares in the tutorial that walks you through the manual computation of a one-way ANOVA. Again, you can check the accuracy of your computations, because the SST is equal to the sum of the SSb and SSw. If you are doing and ANOVA by hand, most of your effort will go into the computation of the SSs.
To compute the mean squares, you simply divide the sum of squares by the appropriate degrees of freedom. So the MSb is equal to SSb divided by dfb, and MSw is equal to SSw divided by dfw.
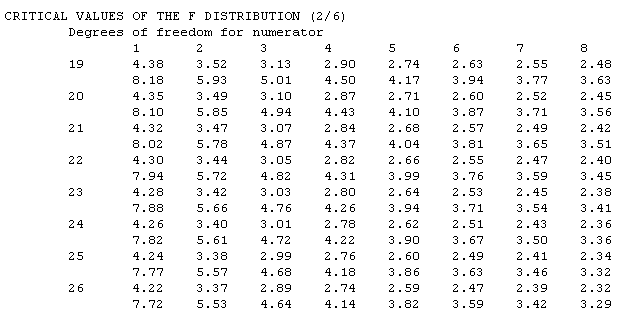
Finally, in a one-way ANOVA, the F is computed by dividing the MSb by the MSw. If you are doing the computation by hand, you would compare the computed value of F against a critical value of F, which is a function of the dfb, dfw, and the alpha level. You would look up the critical value in the F-table. This is a much larger table than some of the other tables that you have used. The table is organized by the df for the numerator and denominator, which in a one-way ANOVA are dfb and dfw, respectively.
A portion of the F table is reproduced below so that we can illustrate how to determine the critical value of F. Assume that we have three groups with 8 people in each group. Then the dfb would equal 3 minus 1 (2) and the dfw would equal 24 minus 3 (21). So in the table below, we would look in the column for 2 degrees of freedom in the numerator and the row with 21 degrees of freedom in the denominator. The number we find is 3.47, which is the critical value of F for an alpha of .05. The number just below 3.47 (in this case, 5.78) is the critical value of F for an alpha of .01.
The formulas for computing the Sums of Squares in a one-way ANOVA are included in the module on how to compute this statistical test by hand. Simply click on the button below to see those formulas and walk through an example.
By the time you get to ANOVAs, you are likely to see the wisdom of using statistical analysis programs for doing the computation. You can see how the program SPSS for Windows would perform this computation by clicking on the other button below.
|
Compute a One-Way ANOVA by hand |
|
Compute a One-Way ANOVA using SPSS |
|
USE THE BROWSER'S |
Probing the Differences
Finding a statistically significant F in a one-way ANOVA tells us only that at least one of the means is statistically different from at least one other mean in the comparison. To find out which means are different will require doing some additional statistical computation, called probing. That is our next topic.