Graziano & Raulin
Research Methods (9th edition)
Computational Procedures for the
Variance and Standard Deviation
To compute the variance and standard deviation, we have to start by computing the Sum of Squares (SS). The Sum of Squares is the sum of the squared distance from the mean, which is the first formula below. This is called the definitional formula because it defines what the sum of squares represents. However, there is an easier computational formula, which is the second formula shown below.
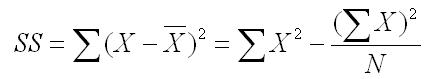
To compute the necessary elements, align your data in one column (labeled X), and then label another column X2. Square each of the numbers in the first column and place the squared value in the second column. Then add both of those columns as shown below.
| X | X2 | |
| 3 | 9 | |
| 1 | 1 | |
| 5 | 25 | |
| 6 | 36 | |
| 3 | 9 | |
| 5 | 25 | |
| 5 | 25 | |
| 5 | 25 | |
| 4 | 16 | |
| 6 | 36 | |
| 3 | 9 | |
| 3 | 9 | |
| Sums | 49 | 225 |
You now have all but one of the values that you need to compute the standard deviation and variance. The last value that you need is the number of scores (N), which in this case is 12. So we plug these numbers into the formulas for SS (sum of squares), s2 (variance), and s (standard deviation), as shown below. Note that all results were rounded to two significant figures.
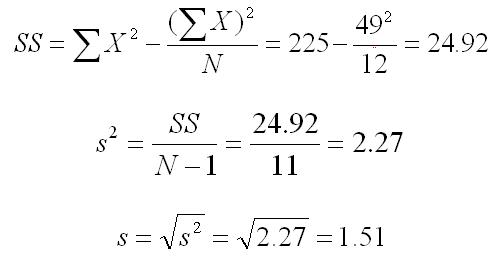
The variance formula divides the sum of squares by what is called the degrees of freedom, which in this case is equal to the number of scores minus 1. Dividing by the degrees of freedom instead of N, as we do in computing the mean, is done because it makes this value of the sample variance an unbiased estimate of the population variance. This concept is explained elsewhere on this website for the interested student.